例子：一阶系统的控制

本节通过一个具体的一阶系统实例，探讨比例控制（Proportional Control）对系统稳定性、稳态误差及瞬态响应的影响，并引出控制工程中核心的“权衡” (Trade-off) 思想。

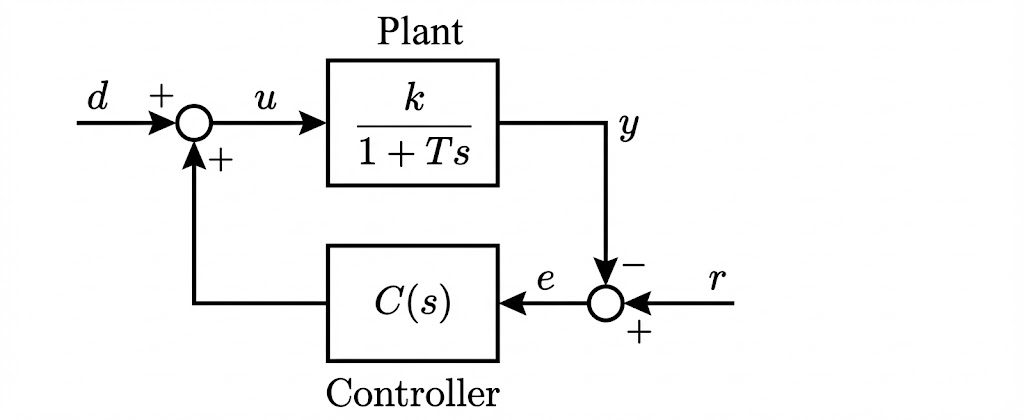
alt text

被控对象 (Plant)：假设被控对象为一阶系统，其传递函数为：

$P (s) = \frac{k}{1 + T s}$

其中 $k$ 为直流增益， $T$ 为时间常数。通常假设 $k, T > 0$ （即对象是开环稳定的）。
控制器 (Controller)：采用最简单的比例控制 (Proportional Control)，即：

$C (s) = K$

其中 $K$ 为可调的常数增益。
控制目标：
1. 稳定性 (Stability)：闭环系统必须稳定。
2. 跟踪 (Tracking)：输出 $y$ 应尽可能接近参考信号 $r$ （即误差 $e$ 小）。
3. 抗扰 (Disturbance Rejection)：抑制扰动 $d$ 对输出的影响。

定义(灵敏度函数)：系统从参考输入 $r$ 到误差 $e$ 的传递函数定义为灵敏度函数 $S (s)$ ：

$S (s) = \frac{1}{1 + P ( s ) C ( s )} = (1 + \frac{k K}{1 + T s})^{- 1} = \frac{1 + T s}{1 + k K + T s}$

定义(闭环传递函数)：系统从参考输入 $r$ 到输出 $y$ 的传递函数为 $G (s)$ （有时也记为 $T (s)$ ，Complementary Sensitivity）：

$G (s) = \frac{P ( s ) C ( s )}{1 + P ( s ) C ( s )} = \frac{k K}{1 + k K + T s}$

注：根据代数关系，恒有 $G (s) + S (s) = 1$ 。

我们将 $G (s)$ 重写为标准的一阶形式：

$G (s) = \frac{k K}{1 + k K} \cdot \frac{1}{1 + τ s}, 其中 τ = \frac{T}{1 + k K}$

此处 $τ$ 为闭环时间常数。

定理(稳定性条件)：系统的极点由特征方程的分母决定： $1 + k K + T s = 0$ 。解得唯一的极点为：

$p_{0} = - \frac{1 + k K}{T}$

为了保证系统稳定（极点位于左半平面，Let $p_{0} < 0$ ），假设 $T > 0$ ，则必须满足：

$1 + k K > 0$

(若 $k, K$ 均为正数，则系统始终稳定)。

分析(阶跃响应)：考察参考信号为单位阶跃信号 $r (t) = 1$ ( $t \geq 0$ ) 时的系统响应。

时域响应 $y_{s t e p} (t)$ ：

$y_{s t e p} (t) = G (0) (1 - e^{- t / τ}) = \frac{k K}{1 + k K} (1 - e^{- \frac{1 + k K}{T} t})$
稳态误差 $e_{ss}$ ：

$e_{ss} = e_{s t e p} (\infty) = 1 - y_{s t e p} (\infty) = 1 - \frac{k K}{1 + k K} = \frac{1}{1 + k K}$

或者直接由 $S (s)$ 计算： $e_{ss} = S (0) \cdot 1 = \frac{1}{1 + k K}$ 。
响应速度：观察 $t = 0$ 处的切线斜率：

$\frac{d}{d t} y_{s t e p} (t)_{t = 0} = \frac{G ( 0 )}{τ} = \frac{k K / ( 1 + k K )}{T / ( 1 + k K )} = \frac{k K}{T}$

我们的设计目标通常是：

从上述公式可以看出，增大控制器增益 $∣ K ∣$ 可以同时实现这两个目标：

然而，增大 $K$ 也会带来严重的副作用：

控制量过大 (Large Control Input)：在 $t = 0$ 时刻，控制输入 $u (t)$ 为：

$u (0) = K \cdot e (0) = K \cdot 1 = K$

如果 $K$ 非常大，初始的控制信号会极大。
- 后果：物理执行机构（如电机、阀门）通常有饱和限制，过大的输入可能导致执行机构饱和（Saturation）甚至物理损坏。
未建模动态导致的失稳 (Instability due to Unmodeled Dynamics)：数学模型 $P (s) = \frac{k}{1 + T s}$ 通常只是真实物理对象的低频近似。真实系统往往包含高频极点（例如传感器延迟、柔性模态等）。
- 后果：虽然理论上对于一阶模型 $K$ 再大也稳定，但在真实系统中，极高的增益 $K$ 会放大高频信号，激发那些未被建模的高频极点，导致闭环系统不稳定。
- 注：这通常需要通过奈奎斯特 (Nyquist) 稳定性判据来深入分析。

结论：控制器的设计不仅是数学优化，更是一种妥协 (Compromise)。我们需要在“提高增益以获得更好性能”和“限制增益以保证安全与鲁棒性”之间找到平衡点。

Keyboard shortcuts