拉普拉斯变换 (Laplace Transform) 概念
定义 (单边拉普拉斯变换) 设 为定义在 上的实函数。其单边拉普拉斯变换定义为:
- :复频率变量,。
- 下限:积分下限取 是为了包含 处的狄拉克 函数(冲击)或其导数。
定义 (收敛域, ROC):使得积分 收敛的 值集合,称为收敛域 (Region of Convergence)。通常形式为 ,其中 为收敛横坐标。
充分条件 (存在性):若 满足以下条件,则 在 处绝对收敛。
- 在任意有限区间上分段连续;
- 具有指数阶 (Exponential order),即存在常数 ,使得 对所有 成立;
拉普拉斯变换的核心性质
微分性质 (Differentiation):
推广至 阶:
证明:利用分部积分法 (Integration by parts),令 ,则 。
在 ROC 内, 足够大使得 。
积分性质 (Integration)
证明:设 ,则 且 。 根据微分性质:
卷积定理 (Convolution Theorem):时域卷积对应频域乘积。这是 LTI 系统 的理论基础。
其中 。
证明:
时不变系统概念与分类
定义(线性时不变系统):考虑线性时不变 (LTI) 系统 ,其状态空间方程 (State-space equations) 描述如下:
- :状态向量 (State), 为系统的阶数 (Order)。例如弹簧伸长度这种无方向的状态一般用实数,例如旋转球体的位置/交流电则可以用复数。
- :输入向量 (Input)。
- :输出向量 (Output)。
- 。实数和复数本质上等价,但是复数用一个维度即可描述旋转,而实数要用两个维度,因此复数维度更低。
系统解析解:使用常数变易法可解出上述系统的解析解
- 称为状态转移矩阵 (State Transition Matrix),它描述了系统在没有外部输入时,初始状态如何随时间自然演化。
- 表示过去所有时刻输入 对当前时刻 的状态产生的累积影响。这是系统的“记忆”体现。
- 零输入响应 (Zero-Input Response):仅由初始能量 引起,与输入无关。
- 零状态响应 (Zero-State Response):仅由外部输入 引起,假设初始状态为零。
根据输入输出分类:SISO (单输入单输出) ;MISO (多输入单输出): ;MIMO(多输入多输出)
根据维度分类:当 为有限值时(即矩阵 为有限维)称之为有限维系统;当 则称之为无限维系统(如延迟线、热传导、波传播等)。
本节我们对系数 进行深入分析,详细讲解 如何决定着系统的动力学行为。
系统定义
定义(线性自治系统):考虑如下一阶常微分方程组:
其中 为状态向量, 为常数矩阵( 可为 或 )。
定理(通解):上述系统的解由矩阵指数给出:
定理(特解):若 是 的特征向量,对应的特征值为 ,且初值 ,则特解为:
注:一般解是这些特解的线性组合(假设 可对角化)。因此,分析 的性质即等同于分析系统行为。
特征值分解
特征值分解:设矩阵 的特征值为复数 ,其中 。根据欧拉公式,解的时间项可以分解为
- 实部 决定了轨道模长的变化趋势(增长或衰减速率)
- (耗散/收敛):因子 (当 )。系统能量耗散,状态沿特征向量方向收敛向原点。
- (发散/膨胀):因子 。系统能量输入,状态沿特征向量方向指数级远离原点。
- (保守):。模长不随时间指数变化(可能保持常数或代数增长)。
- 虚部 决定了系统在相空间中的旋转或振荡频率
- :引入了振荡分量 。在实空间投影下表现为正弦/余弦波;在复空间表现为相位旋转。
- :纯实数特征值,无振荡,系统行为是单调的(直接趋向或远离原点)。
物理模型构建
定义(物理模型):考虑一个质量为 的物体,连接在刚度为 的弹簧和阻尼系数为 的阻尼器上。根据牛顿第二定律:
- 为位移,单位 ,往外为正,往内为负;
- 为质量,单位 ,根据牛顿第二定律 ;
- 为弹簧劲度系数,单位 ,力大小与距离 成正比;
- 为阻尼器,单位 ,力大小与速度 成正比。
推导:假设物体在往右运动,速度为 。则弹簧力往左,大小为 ;阻尼力往左,大小为 。根据牛顿第二定律 :
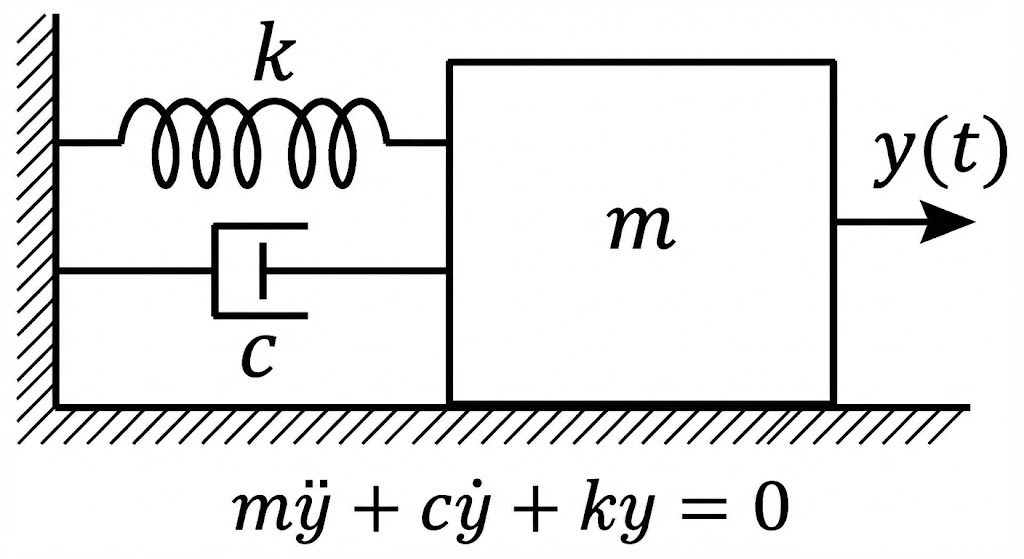
状态空间形式:引入状态向量 。 则 ,且 。 写作矩阵形式 :
无量纲数:取无量纲数阻尼比 ,固有频率 (不是无量纲数)。此时特征方程 的根为:
无量纲数的理解:当 时, 均为实数,此时系统只是单纯的指数衰减;当 时, 是复数,而复数代表着振动,弹簧会来回摆动;当 时,弹簧在振荡与不振荡的临界状态。因此 决定着整个系统的性质。
谱分析与物理现象的对应
我们将根据 的不同取值,分析特征值 的结构及其对应的物理运动。
情形 1 无阻尼振动 (Undamped): (无摩擦)。 特征值:
- 几何意义:纯虚数特征值,对应相图中的中心 (Center)。
- 物理表现:实部 表示能量守恒,振幅不衰减。虚部 表示系统以固有频率进行永恒的简谐振动。
- 轨道是封闭的椭圆。
情形 2 欠阻尼振动 (Underdamped):最常见的情形,小阻尼 。特征值:
- 几何意义:复数特征值且实部为负,对应稳定焦点 (Stable Spiral)。
- 物理表现:实部 ,振幅按 指数衰减。虚部 ,系统仍在往复振动,但频率略低于固有频率 ()。
- 物体在平衡位置附近来回摆动,幅度越来越小。
情形 3 过阻尼 (Overdamped):大阻尼 (如在蜂蜜中运动)。特征值:
- 几何意义:两个负实数特征值,对应稳定节点 (Stable Node)。
- 物理表现:虚部 ,没有振荡,物体不会越过平衡位置来回摆动。实部 ,物体只是缓慢地、单调地滑回平衡位置。
情形 4 负阻尼 (Negative Damping):系统失稳, (系统外界不断输入能量,如风吹过大桥引起的颤振)。特征值实部变号:
- 几何意义:实部为正,对应不稳定焦点/节点。
- 物理表现:实部 ,振幅按指数规律爆炸式增长 ()。
- 这是导致机械结构破坏的主要原因(如塔科马海峡大桥倒塌)。
本节考虑 线性系统概念 中的线性系统。
传递函数的意义在于将复杂的【微积分问题】转换为简单的【代数问题】。
传递函数概念
定义(传递函数):传递函数 定义为零初始条件 下,输入信号的 Laplace 变换 与输出信号的 Laplace 变换 的比值:
命题:上述线性 LTI 系统 的传递函数 为:
其中 是 的特征值组成的集合(Spectrum)。
证明:对输入方程两边同时进行 Laplace 变换,并代入 :
当 时, 可逆,解得状态向量的变换:
对输出方程进行 Laplace 变换,并代入
由此可见,定义 建立了关系 。
输入-输出关系:任意输入 (需具备拉普拉斯变换) 下的输出 的拉普拉斯变换为:
转移函数的性质
性质(有理函数):矩阵 的每个元素都是两个多项式的比值。
证明:根据矩阵求逆公式,对于非奇异矩阵 ,有 ,其中 表示伴随矩阵 (Adjugate matrix)。令 ,则:
- 分母: 是矩阵 的特征多项式,为关于 的 次多项式。
- 分子: 的每个元素是 的代数余子式,即 子矩阵的行列式。因此,其元素均为关于 的多项式,且最高次数不超过 。
由于 均为常数矩阵,它们的线性组合不改变“多项式比值”的性质。因此 的每个元素均为有理函数,且分母为 (或其因子)。
性质(正则):当 时,传递函数趋于有限常值矩阵,即:
证明:考察项 当 时的极限:
当 时,,故 。 因此:
代入 的定义式:
证毕。若 (严格正则),则 。
的极点: 的极点(若 满足对任意 则是极点)是 的子集,即是 的特征值。
证明:根据有理函数性质可知。
本节中考虑 线性系统概念 中定义的线性系统与传递函数。
稳定性定义
定义(稳定性):系统 被称为稳定 (Stable),如果当 时:
其中 为全零矩阵。这意味着若输入 ,从任意初始状态 出发,状态轨迹 均趋于零。
定义 (临界稳定):若 (即特征值位于左半平面或虚轴上),称 LTI 系统为临界稳定 (Marginally Stable)。
稳定性判据:特征值角度
定理(充要条件):系统 是稳定的,当且仅当矩阵 的谱 完全位于左半复平面。
其中开左半平面定义为
证明:利用 Jordan 标准型分解,存在非奇异矩阵 使得 ,其中 为 Jordan 标准型矩阵。状态转移矩阵为:
由于 是块对角矩阵,其中 是对应于特征值 的 Jordan 块,故 。考察单个 阶 Jordan 块 的矩阵指数。对于特征值 ,其 Jordan 块形式为:
根据矩阵指数性质 ,展开可得具体的上三角形式:
可以看出, 的每个元素都是形如 的项的线性组合,其中 。当 时,要使系统稳定(即 ),必须要求矩阵中所有元素趋于零。 利用极限性质:
(即使 随时间增大,只要 有负实部,指数衰减项 最终会主导并使整体趋于零)。因此,系统稳定的充要条件是所有特征值的实部严格小于零,即 。
我们仅考虑矩阵 为实矩阵 () 的情况,其特征多项式 如下,此时系数 均为实数:
定理(必要条件):如果 是实矩阵且稳定的,则其特征多项式的所有系数必须严格大于零。
- 对于 或 ,该条件也是充分的。
- 对于 ,仅检查 是不够的(不充分)。
- 当 时,不存在通用的根式公式来求解多项式的零点,通常需要数值近似。
证明:设 的根为 。由于 稳定,所有 均位于左半开平面。 因为 是实系数多项式,其根要么是实数,要么是共轭复数对。
- 实根 () 对应的因子为 ,系数均为正。
- 共轭复根对 () 对应的因子乘积为 。由于 ,该二次多项式的系数也均为正。
可以分解为上述一阶和二阶因子的乘积。由于具有正系数的多项式之积仍具有正系数,因此 的所有系数 必须严格大于零。
劳斯判据 (Routh Test)
为了在不计算特征值的情况下确定 的稳定性,我们可以使用 劳斯判据 (Routh Test)。仅当已确认所有系数 后才构建劳斯表。若任一系数 ,则 不稳定,无需建表。
为什么 代表 不稳定:上述“必要条件”定理的逆否命题。
劳斯表 (Routh Table):构造如下表格(共 行)
计算公式:后续行的元素由前两行计算得出。第 个元素 的计算公式为:
同理,下一行 由 行(作为前前行)和 行(作为前一行)计算:
定理(Routh Test):系统稳定的充要条件是劳斯表第一列的所有元素均严格大于零。第一列符号改变的次数等于位于右半平面的特征值个数。
证明 (核心思路):劳斯判据的结论并不平凡,它将复平面根的分布问题转化为了代数运算。其证明主要依赖于 柯西辐角原理 (Cauchy's Argument Principle) 和 施图姆定理 (Sturm's Theorem)。
- 辐角原理:考察特征多项式 沿“奈奎斯特围线”(包围整个右半平面)的映射。若系统稳定(无右半平面根),则当 沿虚轴从 变化到 时,相角 的总变化量必须满足特定条件(即净旋转角度与阶数相关)。
- 实部与虚部交替:在虚轴上 ,多项式可写为实部与虚部之和:。可以证明,系统稳定的充要条件等价于 和 的实根在频率轴上交替出现 (Interlacing Property)。
- 欧几里得辗转相除:劳斯表的构造过程(行与行之间的递推计算),本质上是对多项式的偶次部分 和奇次部分 进行欧几里得多项式除法。
结论:劳斯表第一列的符号序列,实际上反映了施图姆序列 (Sturm Sequence) 的符号变化次数。第一列全为正,严格对应于根的完美交替,从而保证所有特征值均在左半平面。
示例 ():考虑特征多项式 ,其劳斯表如下:
计算得:
因此 稳定的充要条件是劳斯表第一列全为正,即:
(注:由于 且 ,这也隐含了 )
定理 (不稳定性判据):如果 不稳定,且劳斯表第一列中的所有数字均非零,则 的不稳定特征值(位于 中)的个数等于劳斯表第一列符号改变的次数。
通常系统不一定用状态空间( 四个矩阵)表示,而是仅用传递函数 表示。
传递函数稳定性
传递函数稳定性依据:我们关心传递函数 的极点,因为 Inverse Laplace Transform 将频域的极点映射为了时域的指数增长/衰减项。对于 的极点
- 震荡项 ():模长恒为 1 (),只决定系统是震荡还是单调,不决定发散。
- 幅值包络 ():若 则 ,稳定。若 则 ,不稳定。
定义(传递函数稳定性):传递函数 被称为稳定 (Stable),如果它满足以下两个条件:
- 在开右半平面 上是有界 (Bounded) 的。
- 在开右半平面 上是解析 (Analytic) 的。
解析保证了有限复平面中无极点,有界保证了无穷远处无极点。
定理(稳定性判据):若 是有理函数,则 是稳定的,当且仅当:
- 它是真分式 (Proper)。
- 其所有极点 (Poles) 均位于开左半平面 。
证明:必要性 ():
- 若 稳定,则在 上有界。假设 不是真分式(即分子阶次 分母阶次),则当 时,,违反有界性条件。故 必须是真分式。
- 若 在 内有极点,则不满足解析性。若 在虚轴 上有极点 ,则当 (从右侧) 时,,违反有界性。故所有极点必须位于 。
充分性 ():
- 若极点均在 ,则 在闭右半平面 (包含虚轴)上无奇点,因此是解析的。
- 由于 是真分式,当 时, 趋于常数(若严格真分式则趋于0)。由于 在 上连续且在无穷远处有界,根据极值定理,它在整个 上是有界的。
注意:如果 在虚轴 上有极点,则当 从右侧趋于该极点时 ,违反有界性,因此是不稳定的。
系统稳定性与传递函数稳定性
定理:如果 是一个稳定的有限维 LTI 系统,则其传递函数 是稳定的。
证明:传递函数由 给定。其极点集合是矩阵 特征值集合 的子集。若 稳定,则 ,故 的极点也均在 。
逆命题通常不成立:
- 如果 不稳定,但由于零极点对消 (Pole-Zero Cancellation) 或系统存在不可控/不可观 (Uncontrollable/Unobservable) 模态, 仍可能表现为稳定。
- 例外:对于最小实现 (Minimal Systems)(即既可控又可观的系统),逆命题成立: 稳定 稳定。
预备知识:电路建模物理基础
基本变量与符号:我们主要关注以下两个随时间 变化的实值函数:
- 电流 (Current) :电荷流动的速率,单位为安培 (A)。
- 电压 (Voltage) :两点间的电势差,单位为伏特 (V)。
元件的伏安特性 (欧姆定律):电路元件的物理特性决定了电压与电流之间的代数或微分关系。
其中 为电阻值。
电感 Inductor:电感是储存磁场能量的元件,具有“惯性”,阻碍电流的变化。其两端电压与流过电流的变化率成正比:
其中 为电感值。
由于 ,即 ,在状态空间模型中,通常选取流过电感的电流作为状态变量,以便通过电压来描述其导数。
电容 Capacitor:电容是储存电场能量的元件。流过电容的电流与电容两端电压的变化率成正比:
其中 为电容值。
由于 ,即 ,在状态空间模型中,通常选取电容两端的电压作为状态变量,以便通过电流来描述其导数。
基尔霍夫电流定律, KCL:对于电路中的任意节点 (Node),流入该节点的电流之和等于流出该节点的电流之和。
基尔霍夫电压定律, KVL:对于电路中的任意闭合回路 (Loop),沿回路绕行一周,电压升高的代数和等于电压降低的代数和。
例子:电路系统的状态空间模型
问题描述:考虑一个包含电阻、电感、电容的电路网络。
- 输入 (Inputs):电压源 和 。
- 输出 (Outputs):电流 和电压 。
- 元件参数: (电阻), (电感), (电容),假设所有参数均为正值 ()。
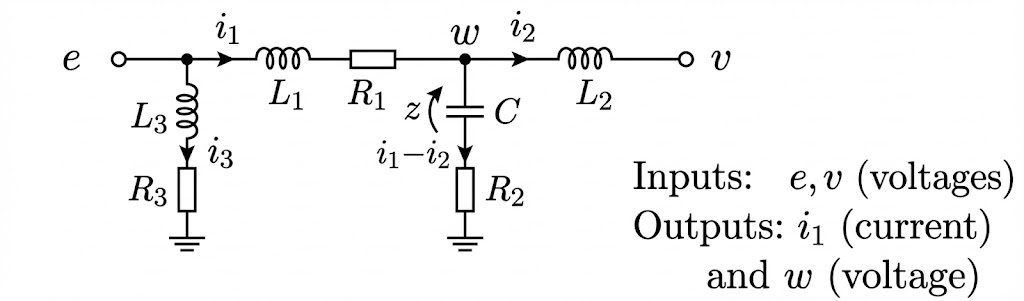
状态变量:选择电感中的电流和电容两端的电压作为状态变量(除非存在代数依赖,本例中不存在)。 定义状态向量 、输入向量 和输出向量 如下:
其中 是电容 两端的电压, 分别为流过各支路的电流。
物理定律:根据基尔霍夫定律 (Kirchhoff's Laws) 及元件的伏安特性方程:
同时,输出方程由 的定义及代数关系 给出。
系统矩阵:将上述方程组写成标准状态空间形式 ,,可得矩阵:
稳定性分析(特征多项式角度):观察矩阵 的块对角结构 (Block Diagonal Structure),其特征多项式 可分解为两个块的特征多项式之积:
其中系数为:
由于电路参数均为正值,显见 且易证 。根据 Routh Test 可知矩阵 是稳定的 (Stable)。
极小性分析 (Minimality):计算传递函数 时,发现矩阵 的最后一行/列、矩阵 的最后一行以及矩阵 的最后一列均对输入输出关系无贡献(Irrelevant)。
- 物理意义:状态 ( 支路)既不影响输出 ,也不影响其他状态变量。尽管输入 驱动了 ,但该支路与其他部分完全解耦。
- 数学结论:包含 的原 4 阶系统不是极小实现 (Not Minimal)。消除 后得到的 3 阶子系统(状态为 )是极小实现。
注:极小性对应于系统的能控性 (Controllability) 和能观性 (Observability)。本例中, 这一状态虽然可能是能控的(受 影响),但对 是不可观的,或者是与其他状态解耦而变得多余。若令 ,系统可能会变得不稳定,具体需进一步分析。
例子:DC Motor
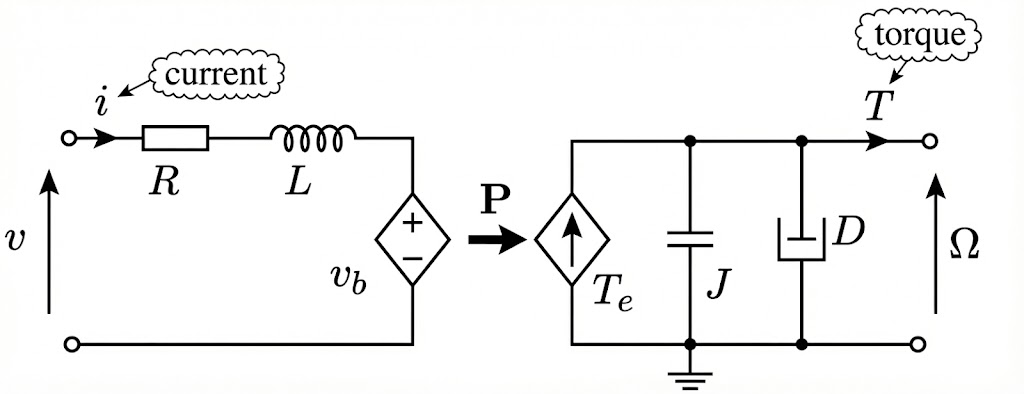
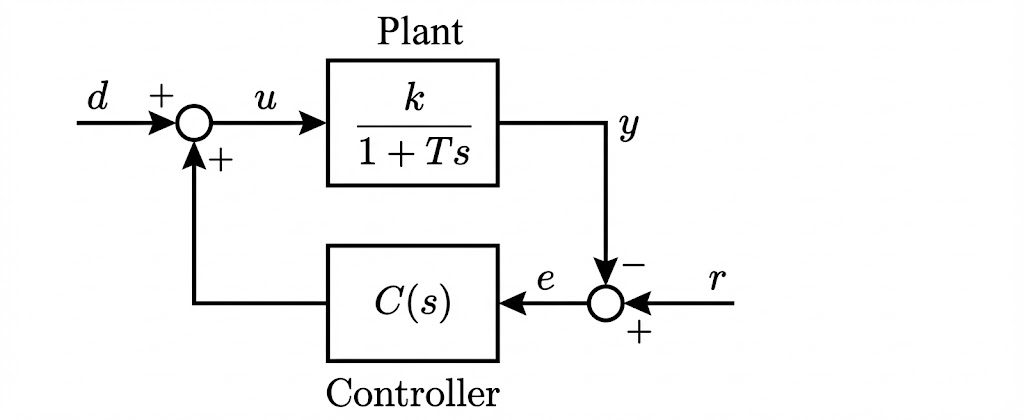
标准反馈连接 (Standard Feedback Connection)
控制系统:下图为频域空间中的控制系统示意图,其中 和 表示频域空间的传递函数(关于 的有理分式)。即 表示 , 表示 。
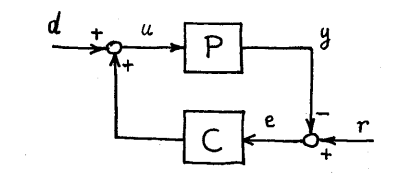
反馈结构:考虑两个传递函数为 (Plant, 被控对象) 和 (Controller, 控制器) 的线性 SISO 系统的反馈连接。根据方框图,系统方程可写作(假设零初始条件):
- : 作用在被控对象上的扰动 (disturbance)
- : 被控对象的输入信号 (input)
- : 被控对象的输出信号 (output)
- : 参考信号 (reference signal)
- : 跟踪误差 (tracking error),
- 等均表示对应变量的拉普拉斯变换
证明:被控对象的输入 由扰动 和控制器输出 叠加而成
误差 定义为参考信号 与输出 () 之差。
将上述整理后的两式写成矩阵形式:
只有在频域空间中才能被写为这样简单的代数系统,在时域中 都是复杂的 ODE。
传递函数:为了求解内部信号 和 ,我们需要对系数矩阵求逆:
计算 矩阵的逆(注意 SISO 系统中 ):
反馈连接的稳定性:被控对象 本身往往是不稳定的(例如战斗机、磁悬浮列车),我们设计控制系统的目的就是用控制器 去把一个不稳定的 变稳定
稳定性分析与零极点对消
当我们把整个控制系统当作一个整体时,我们可能会忽略掉 和 的一些内部作用,而导致系统爆炸。比如 是一个高压锅, 是阀门,正常运作时 能检测到所有压力升高的信号从而打开阀门放气,但如果 的某个零点导致了其忽视了 的某个爆炸极点,这样控制系统就失效了。
定义(零极点对消):若复数 同时满足以下情况,则称在乘积 处发生了 点的零极点对消:
- 是 的极点(或 的极点);
- 是 的零点(或 的零点)。
直观理解:【 极点 - 零点】表示对象要爆炸,控制器在装瞎;【 零点 - 极点】系统对输入不理会,输出端毫无变化时,控制器无限加强。
定义(对消的稳定性):若 (左半平面),称该对消是稳定的。若 (如在虚轴或右半平面),称该对消是不稳定的。
直观理解:【左半平面对消】表示系统本身是稳定的,就算装瞎不去控制它,它也不会爆炸;【右半平面对消】表示系统本身就不稳定,还装瞎不去控制,就会直接爆炸。
定理(稳定性充要条件): 和 的反馈连接是稳定的,当且仅当满足以下两个条件:
- 灵敏度函数稳定: 是稳定的。
- 无不稳定对消:乘积 中不存在不稳定的零极点对消 (pole-zero cancellation)。
证明:设 和 的既约分式表示(互质多项式之比)为:
闭环传递函数矩阵的四个元素在通分后的公共分母(即系统的特征多项式)为:
四个传递函数具体形式为:
必要性 ():若系统稳定,则四个 均稳定。条件 1 显然成立,因为 即为 。假设条件 2 不成立,即存在不稳定对消点 。不妨设 是 的极点 () 且是 的零点 ()。 此时特征多项式 ,即 是特征方程的根。 考查 :由于 是既约的,;同理 既约 implies 。 因此, 的分子在 处不为 0,而分母为 0。这意味着 有一个不稳定的极点 ,系统不稳定。这与假设矛盾,故条件 2 必须成立。
充分性 ():若条件 1 和 2 成立。由条件 1, 稳定,说明 中所有的不稳定根(若存在)必须被 中的零点所抵消。假设 仍有一个不稳定根 。由上一步知,必须有 。若 :代入 的方程,得 。因 既约,,故必有 。这构成了“ 极点与 零点”的不稳定对消,与条件 2 矛盾。若 :同理可推得 ,构成“ 极点与 零点”的不稳定对消,与条件 2 矛盾。
因此, 不可能存在不稳定根。特征多项式稳定意味着矩阵中所有传递函数均稳定。
例 1 (稳定对消): 有极点 , 有零点 。在 处存在对消。由于 ,这是一个稳定的对消。虽然 本身在 处有极点(临界稳定),但对消本身是良态的。
例 2 (不稳定对消): 的极点为 , 的零点为 。在 和 处存在对消。由于这些点不在左半平面,属于不稳定的零极点对消。因此,该反馈连接不稳定。
例 3 (不稳定组件构成稳定系统):。虽然 和 都不稳定(极点在 ),但在 中没有发生零极点对消( 的零点是 ,极点是 ; 无零点,极点是 )。分母 的根实部为负,故该传递函数稳定。反馈连接是稳定的。
术语与控制目标 (Terminology & Goals)
- 环路增益 (Loop Gain):
- 灵敏度函数 (Sensitivity Function):
- 控制目标:我们需要在存在扰动 的情况下实现良好的跟踪(即 ),使误差 尽可能小。误差方程可由之前的矩阵方程导出:
- 目标:使 尽可能小(从而抑制扰动和减小跟踪误差)。
- 约束:减小 的同时不能破坏闭环系统的稳定性。
注 (状态空间解释):如果 和 分别是最小实现 (minimal realization) 的被控对象和控制器,那么反馈系统通常也是最小实现的。在此前提下,仅需检查 的稳定性即可推断系统的内部稳定性。
本节通过一个具体的一阶系统实例,探讨比例控制(Proportional Control)对系统稳定性、稳态误差及瞬态响应的影响,并引出控制工程中核心的“权衡” (Trade-off) 思想。
系统描述 (System Description)
-
被控对象 (Plant):假设被控对象为一阶系统,其传递函数为:
其中 为直流增益, 为时间常数。通常假设 (即对象是开环稳定的)。
-
控制器 (Controller):采用最简单的比例控制 (Proportional Control),即:
其中 为可调的常数增益。
-
控制目标:
- 稳定性 (Stability):闭环系统必须稳定。
- 跟踪 (Tracking):输出 应尽可能接近参考信号 (即误差 小)。
- 抗扰 (Disturbance Rejection):抑制扰动 对输出的影响。
闭环特性分析
定义(灵敏度函数):系统从参考输入 到误差 的传递函数定义为灵敏度函数 :
定义(闭环传递函数):系统从参考输入 到输出 的传递函数为 (有时也记为 ,Complementary Sensitivity):
注:根据代数关系,恒有 。
我们将 重写为标准的一阶形式:
此处 为闭环时间常数。
性能与稳定性分析
定理(稳定性条件): 系统的极点由特征方程的分母决定:。 解得唯一的极点为:
为了保证系统稳定(极点位于左半平面,Let ),假设 ,则必须满足:
(若 均为正数,则系统始终稳定)。
分析(阶跃响应): 考察参考信号为单位阶跃信号 () 时的系统响应。
-
时域响应 :
-
稳态误差 :
或者直接由 计算:。
-
响应速度: 观察 处的切线斜率:
增益设计的权衡 (The Trade-off)
我们的设计目标通常是:
- 小的稳态误差 ()
- 快的响应速度 ()
从上述公式可以看出,增大控制器增益 可以同时实现这两个目标:
- 当 时,。
- 当 时,(响应变快)。
然而,增大 也会带来严重的副作用:
-
控制量过大 (Large Control Input): 在 时刻,控制输入 为:
如果 非常大,初始的控制信号会极大。
- 后果:物理执行机构(如电机、阀门)通常有饱和限制,过大的输入可能导致执行机构饱和(Saturation)甚至物理损坏。
-
未建模动态导致的失稳 (Instability due to Unmodeled Dynamics): 数学模型 通常只是真实物理对象的低频近似。真实系统往往包含高频极点(例如传感器延迟、柔性模态等)。
- 后果:虽然理论上对于一阶模型 再大也稳定,但在真实系统中,极高的增益 会放大高频信号,激发那些未被建模的高频极点,导致闭环系统不稳定。
- 注:这通常需要通过奈奎斯特 (Nyquist) 稳定性判据来深入分析。
结论:控制器的设计不仅是数学优化,更是一种妥协 (Compromise)。我们需要在“提高增益以获得更好性能”和“限制增益以保证安全与鲁棒性”之间找到平衡点。
与连续时间系统不同,离散时间时滞系统可以通过状态增广 (State Augmentation) 转化为一个无时滞的高维系统。虽然这会增加计算维度,但它提供了一个非常直观的分析框架。
基础模型与状态增广
线性定常时滞系统:考虑如下具有常数时滞 的线性离散系统:
为状态变量,需要给出一段历史数据 作为初始条件。
定义(增广状态向量):为了消除显式的时滞项,我们定义一个新的“增广状态” ,包含当前状态和过去 步的状态:
定理(无时滞系统转换):原系统可以重写为如下形式的无时滞系统:
其中,增广矩阵 具有如下的伴随形式 (Companion Form):
证明:我们需要验证 是否真的等于 。左边根据定义, 是将时间向前推一步:
右边进行矩阵乘法运算:
- 第 1 行: 。这正是原系统的动力学方程。
- 第 2 行: 。这是一个恒等式(当前时刻的 变成了下一时刻的“过去一步状态”)。
- 第 3 行: 。
- 以此类推,直到最后一行。
离散时滞系统在本质上是有限维的,系统维数从 变为 。
稳定性分析
渐进稳定性:对于离散系统,渐近稳定 (Asymptotically Stable) 意味着对于任意小的初始条件,随着时间推移 ,状态范数趋于零,即
Lyapunov 方法: 系统渐近稳定的充要条件是存在一个正定矩阵 ,使得 Lyapunov 函数 满足:
虽然增广法将问题简化为标准的 LTI 系统分析,但如果时滞 很大,矩阵 的维数会急剧膨胀,导致计算极其复杂。如果时滞参数 是未知的或不确定的,增广法也会变得难以应用。
时变时滞与切换系统 (Time-Varying Delays & Switched Systems)
定义(时变时滞):当时滞不是常数,而是随时间变化的
难点:当时滞 变成随时间变化的 () 时,常数矩阵 就不存在了
线性切换系统:时变时滞系统中增广矩阵 不再是常数矩阵,而是随 的取值在变化。这可以被建模为一个线性切换系统 (Linear Switched System):
其中 。根据 的不同取值,系统矩阵在 个可能的矩阵 之间切换。
离散时变时滞系统的稳定性问题,可以转化为任意切换规则下的线性切换系统的稳定性问题。
传递函数法
传递函数法:对于多时滞、含输入的系统:
其中 。
Z变换:通过 Z 变换 (),可以得到传递函数矩阵 :
的每一项都是 的多项式的商。
基于 Section 6.1.3 - 6.1.4 (直接 Lyapunov 方法与 LMI)
1. 为什么要用“直接方法”?
在第一部分中,我们通过增广法将时滞系统转化为无时滞的高维系统。虽然理论上精确,但存在维数灾难:当且仅当时滞 较小时适用。如果 ,系统维数就会翻 20 倍,计算极其缓慢。
直接 Lyapunov 方法 (Direct Lyapunov Method) 克服了这个问题。它不增加系统状态的维数,而是通过构造复杂的Lyapunov-Krasovskii 泛函 (LKF) 或使用 Lyapunov-Razumikhin 方法 来导出稳定性条件。这些条件通常是充分条件,以 LMI (线性矩阵不等式) 的形式给出。
2. 时滞独立稳定性 (Delay-Independent Stability)
核心思想:无论时滞 有多大,系统都保持稳定。这是一种非常保守(强)的稳定性。
2.1 基于 Lyapunov-Razumikhin 方法
对于时变时滞系统 ,我们寻找一个标准的 Lyapunov 函数 。 为了处理时滞项,Razumikhin 定理引入了一个条件:不需要 在所有时刻都下降,只需要在当前时刻的能量“即使考虑到过去的历史也是最大”的时候下降即可。
LMI 条件 (Proposition 6.1): 给定调节标量 ,如果存在正定矩阵 满足以下 LMI,则系统对任意时滞渐近稳定:
- 注:这种条件通常只适用于 本身就是稳定矩阵(Schur Matrix)的情况。
3. 时滞依赖稳定性 (Delay-Dependent Stability)
核心思想:系统只在时滞小于某个上限 () 时稳定。这是工程中最实用的分析。
3.1 Lyapunov-Krasovskii 泛函 (LKF) 的构造
这是离散时滞分析中最关键的部分。一个经典的 LKF 通常包含三部分:
- : 标准的二次型能量。
- : 这对应于连续时间中的积分项 。它“存储”了过去 步的状态能量。
- : 其中 是状态的差分(类似于速度)。 这对应于连续时间中的 。
- 作用: 这一项对于利用 Jensen 不等式导出较少保守性的条件至关重要。
3.2 关键数学工具
为了处理差分项 中的复杂求和,我们需要用到两个核心不等式技术:
-
Jensen 不等式 (离散形式): 用于将求和项的二次型转化为求和后项的二次型(放大不等式,为了获得负定的上界)。
它把中间的所有差分项“压缩”成了首尾两项 和 的差。
-
倒凸方法 (Reciprocally Convex Approach): 当处理时变时滞 时,求和区间会被切分为 和 两段。倒凸方法用于处理形如 的各项,使得最终的 LMI 能够覆盖所有可能的时变时滞,且比简单的放缩更精确。
3.3 主要结论 (Theorem 6.1)
基于上述 LKF 和不等式技术,系统在 范围内渐近稳定的充分条件是存在矩阵 等满足特定的 LMI(形如 )。
- 具体矩阵形式见文稿中的式 (6.16) 或 (6.18)。
- 这些 LMI 可以直接在 MATLAB 中使用 YALMIP 或 LMI Toolbox 求解。
4. -增益分析 (性能分析)
除了稳定性,我们还关心系统在外部扰动 下的表现。
-
系统模型:
-
-增益 (): 我们希望找到最小的 ,使得对于零初始条件,输出能量总小于输入扰动能量的 倍:
-
LMI 条件: 通过在 Lyapunov 差分中加入性能指标项 ,可以推导出包含 的 LMI (6.24)。这允许我们在保证稳定的同时,优化系统的抗干扰能力。