Control Theory

物理模型构建

定义(物理模型)：考虑一个质量为 $m$ 的物体，连接在刚度为 $k$ 的弹簧和阻尼系数为 $c$ 的阻尼器上。根据牛顿第二定律：

$$m\ddot{y}+c\dot{y}+ky=0$$

• $y(t)$ 为位移，单位 $m$，往外为正，往内为负；
• $m$ 为质量，单位 $kg$，根据牛顿第二定律 $F=ma$；
• $k$ 为弹簧劲度系数，单位 $kg/s^2$，力大小与距离 $y(t)$ 成正比；
• $c$ 为阻尼器，单位 $kg/s$，力大小与速度 $\dot{y}(t)$ 成正比。

推导：假设物体在往右运动，速度为 $\dot{y}$。则弹簧力往左，大小为 $ky(t)$；阻尼力往左，大小为 $c\dot{y}(t)$。根据牛顿第二定律 $F=ma$：

$$-ky-c\dot{y}=m\ddot{y}\Rightarrow m\ddot{y}+c\dot{y}+ky=0.$$

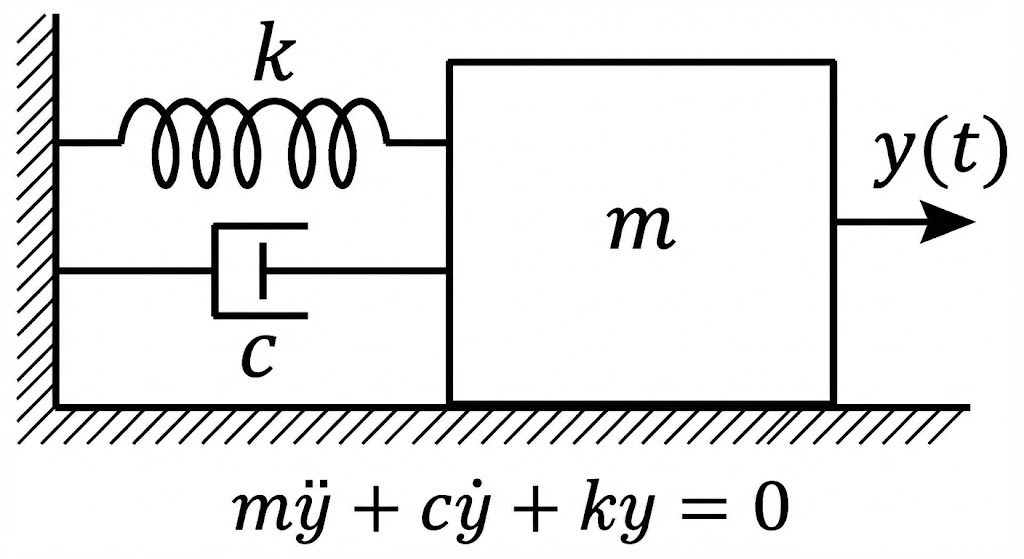
状态空间形式：引入状态向量 $x=\left(\begin{array}{c}y\\ \dot{y}\end{array}\right)=\left(\begin{array}{c}\text{位置}\\ \text{速度}\end{array}\right)$。 则 ${\dot{x}}_1=x_2$，且 ${\dot{x}}_2=-\frac{k}{m}{x}_1-\frac{c}{m}{x}_2$。 写作矩阵形式 $\dot{x}=Ax$：

$$\dot{x}=Ax=\left(\begin{array}{cc}0& 1\\ -\frac{k}{m}& -\frac{c}{m}\end{array}\right)x.$$

无量纲数：取无量纲数阻尼比 $\zeta =\frac{c}{2\sqrt{km}}$，固有频率 ${\omega }_n=\sqrt{\frac{k}{m}}$ （不是无量纲数）。此时特征方程 $\det (\lambda I-A)={\lambda }^2+2\zeta {\omega }_n\lambda +{\omega }_n^2=0$ 的根为：

$${\lambda }_{1,2}=-\zeta {\omega }_n\pm {\omega }_n\sqrt{{\zeta }^2-1}$$

$\zeta$ 无量纲数的理解：当 $\zeta >1$ 时，$\lambda$ 均为实数，此时系统只是单纯的指数衰减；当 $\zeta <1$ 时，$\lambda$ 是复数，而复数代表着振动，弹簧会来回摆动；当 $\zeta =1$ 时，弹簧在振荡与不振荡的临界状态。因此 $\zeta$ 决定着整个系统的性质。

谱分析与物理现象的对应

我们将根据 $\zeta$ 的不同取值，分析特征值 $\lambda =\alpha +i\beta$ 的结构及其对应的物理运动。

情形 1 无阻尼振动 (Undamped)：$c=0⟹\zeta =0$ (无摩擦)。 特征值：

$$\lambda =\pm i{\omega }_n\Rightarrow \alpha =0,\beta ={\omega }_n$$

• 几何意义：纯虚数特征值，对应相图中的中心 (Center)。
• 物理表现：实部 $\alpha =0$ 表示能量守恒，振幅不衰减。虚部 $\beta ={\omega }_n$ 表示系统以固有频率进行永恒的简谐振动。
• 轨道是封闭的椭圆。

情形 2 欠阻尼振动 (Underdamped)：最常见的情形，小阻尼 $0<\zeta <1$。特征值：

$$\lambda =-\zeta {\omega }_n\pm i\underset{{\omega }_d}{\underbrace{{\omega }_n\sqrt{1-{\zeta }^2}}}\Rightarrow \alpha =-\zeta {\omega }_n<0,\beta ={\omega }_d\ne 0$$

• 几何意义：复数特征值且实部为负，对应稳定焦点 (Stable Spiral)。
• 物理表现：实部 $\alpha <0$，振幅按 $e^{-\zeta {\omega }_{n}t}$ 指数衰减。虚部 $\beta \ne 0$，系统仍在往复振动，但频率略低于固有频率 (${\omega }_d<{\omega }_n$)。
• 物体在平衡位置附近来回摆动，幅度越来越小。

情形 3 过阻尼 (Overdamped)：大阻尼 $\zeta >1$ (如在蜂蜜中运动)。特征值：

$${\lambda }_{1,2}=-\zeta {\omega }_n\pm {\omega }_n\sqrt{{\zeta }^2-1}\Rightarrow {\alpha }_{1,2}<0,\beta =0$$

• 几何意义：两个负实数特征值，对应稳定节点 (Stable Node)。
• 物理表现：虚部 $\beta =0$，没有振荡，物体不会越过平衡位置来回摆动。实部 $\alpha <0$，物体只是缓慢地、单调地滑回平衡位置。

情形 4 负阻尼 (Negative Damping)：系统失稳，$c<0$ (系统外界不断输入能量，如风吹过大桥引起的颤振)。特征值实部变号：

$$\alpha >0$$

• 几何意义：实部为正，对应不稳定焦点/节点。
• 物理表现：实部 $\alpha >0$，振幅按指数规律爆炸式增长 ($e^{\alpha t}\to \infty$)。
• 这是导致机械结构破坏的主要原因（如塔科马海峡大桥倒塌）。