Control Theory

标准反馈连接 (Standard Feedback Connection)

控制系统：下图为频域空间中的控制系统示意图，其中 $P$ 和 $C$ 表示频域空间的传递函数（关于 $s$ 的有理分式）。即 $s$ 表示 $\frac{\mathrm{d}}{\mathrm{d}t}$，$1/s$ 表示 $\int \mathrm{d}t$。

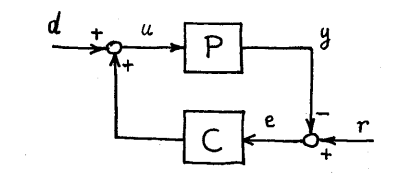
反馈结构：考虑两个传递函数为 $P$ (Plant, 被控对象) 和 $C$ (Controller, 控制器) 的线性 SISO 系统的反馈连接。根据方框图，系统方程可写作（假设零初始条件）：

$$\left[\begin{array}{c}\hat{d}\\ \hat{r}\end{array}\right]=\left[\begin{array}{cc}1& -C\\ P& 1\end{array}\right]\left[\begin{array}{c}\hat{u}\\ \hat{e}\end{array}\right]$$

• $d$: 作用在被控对象上的扰动 (disturbance)
• $u$: 被控对象的输入信号 (input)
• $y$: 被控对象的输出信号 (output)
• $r$: 参考信号 (reference signal)
• $e$: 跟踪误差 (tracking error), $e=r-y$
• $\hat{d},\hat{r},\hat{u},\hat{e}$ 等均表示对应变量的拉普拉斯变换

证明：被控对象的输入 $u$ 由扰动 $d$ 和控制器输出 $Ce$ 叠加而成

$$\hat{u}=\hat{d}+C\hat{e}⟹\hat{d}=\hat{u}-C\hat{e}$$

误差 $e$ 定义为参考信号 $r$ 与输出 $y$ ($=Pu$) 之差。

$$\hat{e}=\hat{r}-P\hat{u}⟹\hat{r}=P\hat{u}+\hat{e}$$

将上述整理后的两式写成矩阵形式：

$$\left[\begin{array}{c}\hat{d}\\ \hat{r}\end{array}\right]=\left[\begin{array}{cc}1& -C\\ P& 1\end{array}\right]\left[\begin{array}{c}\hat{u}\\ \hat{e}\end{array}\right]$$

只有在频域空间中才能被写为这样简单的代数系统，在时域中 $P,C$ 都是复杂的 ODE。

传递函数：为了求解内部信号 $\hat{u}$ 和 $\hat{e}$，我们需要对系数矩阵求逆：

$$\left[\begin{array}{c}\hat{u}\\ \hat{e}\end{array}\right]={\left[\begin{array}{cc}1& -C\\ P& 1\end{array}\right]}^{-1}\left[\begin{array}{c}\hat{d}\\ \hat{r}\end{array}\right]$$

计算 $2\times 2$ 矩阵的逆（注意 SISO 系统中 $PC=CP$）：

$${\left[\begin{array}{cc}1& -C\\ P& 1\end{array}\right]}^{-1}=(1+PC{)}^{-1}\left[\begin{array}{cc}1& C\\ -P& 1\end{array}\right]=\left[\begin{array}{cc}(1+PC{)}^{-1}& C(1+PC{)}^{-1}\\ -P(1+CP{)}^{-1}& (1+PC{)}^{-1}\end{array}\right]$$

反馈连接的稳定性：被控对象 $P$ 本身往往是不稳定的（例如战斗机、磁悬浮列车），我们设计控制系统的目的就是用控制器 $C$ 去把一个不稳定的 $P$ 变稳定

稳定性分析与零极点对消

当我们把整个控制系统当作一个整体时，我们可能会忽略掉 $P$ 和 $C$ 的一些内部作用，而导致系统爆炸。比如 $P$ 是一个高压锅，$C$ 是阀门，正常运作时 $C$ 能检测到所有压力升高的信号从而打开阀门放气，但如果 $C$ 的某个零点导致了其忽视了 $P$ 的某个爆炸极点，这样控制系统就失效了。

定义(零极点对消)：若复数 $z$ 同时满足以下情况，则称在乘积 $PC$ 处发生了 $z$ 点的零极点对消：

• $z$ 是 $P$ 的极点（或 $C$ 的极点）；
• $z$ 是 $C$ 的零点（或 $P$ 的零点）。

直观理解：【$P$ 极点 - $C$ 零点】表示对象要爆炸，控制器在装瞎；【$P$ 零点 - $C$ 极点】系统对输入不理会，输出端毫无变化时，控制器无限加强。

定义(对消的稳定性)：若 $z\in {\mathbb{C}}_{-}$（左半平面），称该对消是稳定的。若 $z\notin {\mathbb{C}}_{-}$（如在虚轴或右半平面），称该对消是不稳定的。

直观理解：【左半平面对消】表示系统本身是稳定的，就算装瞎不去控制它，它也不会爆炸；【右半平面对消】表示系统本身就不稳定，还装瞎不去控制，就会直接爆炸。

定理(稳定性充要条件)：$P$ 和 $C$ 的反馈连接是稳定的，当且仅当满足以下两个条件：

• 灵敏度函数稳定：$(1+PC{)}^{-1}$ 是稳定的。
• 无不稳定对消：乘积 $PC$ 中不存在不稳定的零极点对消 (pole-zero cancellation)。

证明：设 $P(s)$ 和 $C(s)$ 的既约分式表示（互质多项式之比）为：

$$P(s)=\frac{N_p(s)}{D_p(s)},C(s)=\frac{N_c(s)}{D_c(s)}$$

闭环传递函数矩阵的四个元素在通分后的公共分母（即系统的特征多项式）为：

$$\Delta (s)=D_p(s)D_c(s)+N_p(s)N_c(s)$$

四个传递函数具体形式为：

$$\begin{array}{rlr}& H_{11}=(1+PC{)}^{-1}=\frac{D_p{D}_c}{\Delta },& H_{12}=C(1+PC{)}^{-1}=\frac{D_p{N}_c}{\Delta }\\ & H_{21}=-P(1+PC{)}^{-1}=\frac{-N_p{D}_c}{\Delta },& H_{22}=(1+PC{)}^{-1}=H_{11}\end{array}$$

必要性 ($\Rightarrow$)：若系统稳定，则四个 $H_{ij}$ 均稳定。条件 1 显然成立，因为 $H_{11}$ 即为 $(1+PC{)}^{-1}$。假设条件 2 不成立，即存在不稳定对消点 $\lambda \in {\mathbb{C}}_{\ge 0}$。不妨设 $\lambda$ 是 $P$ 的极点 ($D_p(\lambda )=0$) 且是 $C$ 的零点 ($N_c(\lambda )=0$)。 此时特征多项式 $\Delta (\lambda )=0\cdot D_c+N_p\cdot 0=0$，即 $\lambda$ 是特征方程的根。 考查 $H_{21}=\frac{-N_p{D}_c}{\Delta }$：由于 $P$ 是既约的，$D_p(\lambda )=0⟹N_p(\lambda )\ne 0$；同理 $C$ 既约 implies $D_c(\lambda )\ne 0$。 因此，$H_{21}$ 的分子在 $\lambda$ 处不为 0，而分母为 0。这意味着 $H_{21}$ 有一个不稳定的极点 $\lambda$，系统不稳定。这与假设矛盾，故条件 2 必须成立。

充分性 ($\Leftarrow$)：若条件 1 和 2 成立。由条件 1，$(1+PC{)}^{-1}=\frac{D_p{D}_c}{\Delta }$ 稳定，说明 $\Delta (s)$ 中所有的不稳定根（若存在）必须被 $D_p{D}_c$ 中的零点所抵消。假设 $\Delta (s)$ 仍有一个不稳定根 $\lambda$。由上一步知，必须有 $D_p(\lambda )D_c(\lambda )=0$。若 $D_p(\lambda )=0$：代入 $\Delta (\lambda )=0$ 的方程，得 $N_p(\lambda )N_c(\lambda )=0$。因 $P$ 既约，$N_p(\lambda )\ne 0$，故必有 $N_c(\lambda )=0$。这构成了“$P$ 极点与 $C$ 零点”的不稳定对消，与条件 2 矛盾。若 $D_c(\lambda )=0$：同理可推得 $N_p(\lambda )=0$，构成“$C$ 极点与 $P$ 零点”的不稳定对消，与条件 2 矛盾。

因此，$\Delta (s)$ 不可能存在不稳定根。特征多项式稳定意味着矩阵中所有传递函数均稳定。

例 1 (稳定对消)：$P$ 有极点 $s=-1$，$C$ 有零点 $s=-1$。在 $z=-1$ 处存在对消。由于 $-1\in {\mathbb{C}}_{-}$，这是一个稳定的对消。虽然 $C(s)$ 本身在 $\pm i$ 处有极点（临界稳定），但对消本身是良态的。

$$P(s)=\frac{s}{(s+1)(s-2)},C(s)=\frac{5(s+1)}{s^2+1}$$

例 2 (不稳定对消)：$P$ 的极点为 $\pm i$，$C$ 的零点为 $\pm i$。在 $z=i$ 和 $z=-i$ 处存在对消。由于这些点不在左半平面，属于不稳定的零极点对消。因此，该反馈连接不稳定。

$$P(s)=\frac{2s}{s^2+1},C(s)=\frac{s^2+1}{(s+2)(s+100)}$$

例 3 (不稳定组件构成稳定系统)：$PC=\frac{3s}{(s-1{)}^2}$。虽然 $P$ 和 $C$ 都不稳定（极点在 $1$），但在 $PC$ 中没有发生零极点对消（$P$ 的零点是 $0$，极点是 $1$；$C$ 无零点，极点是 $1$）。分母 $s^2+s+1$ 的根实部为负，故该传递函数稳定。反馈连接是稳定的。

$$P(s)=\frac{3s}{s-1},C(s)=\frac{1}{s-1}$$

$$(1+PC{)}^{-1}=\frac{1}{1+\frac{3s}{(s-1{)}^2}}=\frac{(s-1{)}^2}{(s-1{)}^2+3s}=\frac{s^2-2s+1}{s^2+s+1}$$

术语与控制目标 (Terminology & Goals)

• 环路增益 (Loop Gain): $L(s)=P(s)C(s)$
• 灵敏度函数 (Sensitivity Function): $S(s)=(1+P(s)C(s){)}^{-1}$
• 控制目标：我们需要在存在扰动 $d$ 的情况下实现良好的跟踪（即 $y\approx r$），使误差 $e$ 尽可能小。误差方程可由之前的矩阵方程导出：

$$\hat{e}=-P(1+PC{)}^{-1}\hat{d}+(1+PC{)}^{-1}\hat{r}=-PS\hat{d}+S\hat{r}$$

• 目标：使 $S$ 尽可能小（从而抑制扰动和减小跟踪误差）。
• 约束：减小 $S$ 的同时不能破坏闭环系统的稳定性。

注 (状态空间解释)：如果 $P$ 和 $C$ 分别是最小实现 (minimal realization) 的被控对象和控制器，那么反馈系统通常也是最小实现的。在此前提下，仅需检查 $(1+PC{)}^{-1}$ 的稳定性即可推断系统的内部稳定性。