Control Theory

预备知识：电路建模物理基础

基本变量与符号：我们主要关注以下两个随时间 $t$ 变化的实值函数：

• 电流 (Current) $i(t)$：电荷流动的速率，单位为安培 (A)。
• 电压 (Voltage) $v(t)$：两点间的电势差，单位为伏特 (V)。

元件的伏安特性 (欧姆定律)：电路元件的物理特性决定了电压与电流之间的代数或微分关系。

$$v(t)=R\cdot i(t)$$

其中 $R>0$ 为电阻值。

电感 Inductor：电感是储存磁场能量的元件，具有“惯性”，阻碍电流的变化。其两端电压与流过电流的变化率成正比：

$$v(t)=L\cdot \frac{di(t)}{dt}=L\dot{i}(t)$$

其中 $L>0$ 为电感值。

由于 $L\dot{i}=v$，即 $\dot{i}=\frac{1}{L}v$，在状态空间模型中，通常选取流过电感的电流作为状态变量，以便通过电压来描述其导数。

电容 Capacitor：电容是储存电场能量的元件。流过电容的电流与电容两端电压的变化率成正比：

$$i(t)=C\cdot \frac{dv(t)}{dt}=C\dot{v}(t)$$

其中 $C>0$ 为电容值。

由于 $C\dot{v}=i$，即 $\dot{v}=\frac{1}{C}i$，在状态空间模型中，通常选取电容两端的电压作为状态变量，以便通过电流来描述其导数。

基尔霍夫电流定律, KCL：对于电路中的任意节点 (Node)，流入该节点的电流之和等于流出该节点的电流之和。

$$\sum i_{\text{in}}=\sum i_{\text{out}}\text{或}\sum _k{i}_k(t)=0$$

基尔霍夫电压定律, KVL：对于电路中的任意闭合回路 (Loop)，沿回路绕行一周，电压升高的代数和等于电压降低的代数和。

$$\sum v_{\text{rise}}=\sum v_{\text{drop}}\text{或}\sum _k{v}_k(t)=0$$

例子：电路系统的状态空间模型

问题描述：考虑一个包含电阻、电感、电容的电路网络。

• 输入 (Inputs)：电压源 $e$ 和 $v$。
• 输出 (Outputs)：电流 $i_1$ 和电压 $w$。
• 元件参数：$R_1,R_2,R_3$ (电阻), $L_1,L_2,L_3$ (电感), $C$ (电容)，假设所有参数均为正值 ($>0$)。

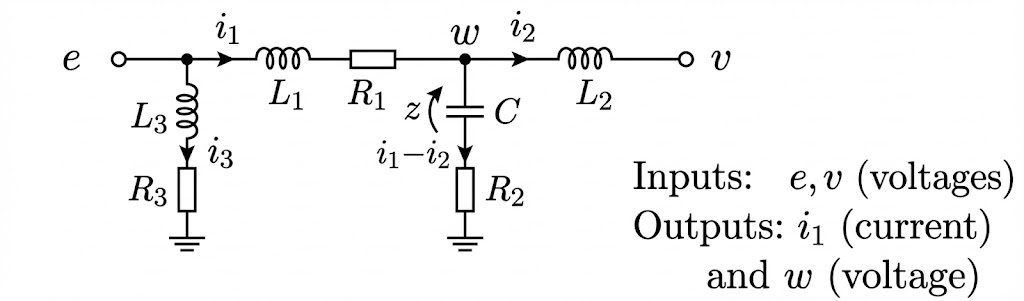
状态变量：选择电感中的电流和电容两端的电压作为状态变量（除非存在代数依赖，本例中不存在）。 定义状态向量 $x$、输入向量 $u$ 和输出向量 $y$ 如下：

$$x=\left[\begin{array}{c}{i}_1\\ i_2\\ z\\ i_3\end{array}\right],u=\left[\begin{array}{c}e\\ v\end{array}\right],y=\left[\begin{array}{c}{i}_1\\ w\end{array}\right]$$

其中 $z$ 是电容 $C$ 两端的电压，$i_1,i_2,i_3$ 分别为流过各支路的电流。

物理定律：根据基尔霍夫定律 (Kirchhoff's Laws) 及元件的伏安特性方程：

• $e-w=L_1{\dot{i}}_1+R_1{i}_1$
• $w-v=L_2{\dot{i}}_2$
• $w=z+R_2(i_1-i_2)$
• $i_1-i_2=C\dot{z}$
• $e=L_3{\dot{i}}_3+R_3{i}_3$

$$\{\begin{array}{ll}{L}_1{\dot{i}}_1& =-R_1{i}_1-R_2{i}_1+R_2{i}_2-z+e\\ L_2{\dot{i}}_2& =R_2{i}_1-R_2{i}_2+z-v\\ C\dot{z}& =i_1-i_2\\ L_3{\dot{i}}_3& =-R_3{i}_3+e\end{array}$$

同时，输出方程由 $y$ 的定义及代数关系 $w=z+R_2(i_1-i_2)$ 给出。

系统矩阵：将上述方程组写成标准状态空间形式 $\dot{x}=Ax+Bu$，$y=Cx+Du$，可得矩阵：

$$A=\left[\begin{array}{cccc}-\frac{R_1+R_2}{L_1}& \frac{R_2}{L_1}& -\frac{1}{L_1}& 0\\ \frac{R_2}{L_2}& -\frac{R_2}{L_2}& \frac{1}{L_2}& 0\\ \frac{1}{C}& -\frac{1}{C}& 0& 0\\ 0& 0& 0& -\frac{R_3}{L_3}\end{array}\right],B=\left[\begin{array}{cc}\frac{1}{L_1}& 0\\ 0& -\frac{1}{L_2}\\ 0& 0\\ \frac{1}{L_3}& 0\end{array}\right]$$

$$C=\left[\begin{array}{cccc}1& 0& 0& 0\\ R_2& -R_2& 1& 0\end{array}\right],D=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]$$

稳定性分析(特征多项式角度)：观察矩阵 $A$ 的块对角结构 (Block Diagonal Structure)，其特征多项式 $p(s)=\det (sI-A)$ 可分解为两个块的特征多项式之积：

$$p(s)=(s^3+a_2{s}^2+a_{1}s+a_0)\left(s+\frac{R_3}{L_3}\right)$$

其中系数为：

$$\begin{array}{rl}{a}_2& =\frac{R_1+R_2}{L_1}+\frac{R_2}{L_2}\\ a_1& =\frac{R_1{R}_2}{L_1{L}_2}+\frac{1}{L_{1}C}+\frac{1}{L_{2}C}\\ a_0& =\frac{R_1}{L_1{L}_{2}C}\end{array}$$

由于电路参数均为正值，显见 $a_0,a_1,a_2>0$ 且易证 $a_1{a}_2>a_0$。根据 Routh Test 可知矩阵 $A$ 是稳定的 (Stable)。

极小性分析 (Minimality)：计算传递函数 $G(s)$ 时，发现矩阵 $A$ 的最后一行/列、矩阵 $B$ 的最后一行以及矩阵 $C$ 的最后一列均对输入输出关系无贡献（Irrelevant）。

• 物理意义：状态 $i_3$（$L_3,R_3$ 支路）既不影响输出 $y$，也不影响其他状态变量。尽管输入 $e$ 驱动了 $i_3$，但该支路与其他部分完全解耦。
• 数学结论：包含 $i_3$ 的原 4 阶系统不是极小实现 (Not Minimal)。消除 $L_3,R_3$ 后得到的 3 阶子系统（状态为 $i_1,i_2,z$）是极小实现。

注：极小性对应于系统的能控性 (Controllability) 和能观性 (Observability)。本例中，$i_3$ 这一状态虽然可能是能控的（受 $e$ 影响），但对 $y$ 是不可观的，或者是与其他状态解耦而变得多余。若令 $R_1=0$，系统可能会变得不稳定，具体需进一步分析。

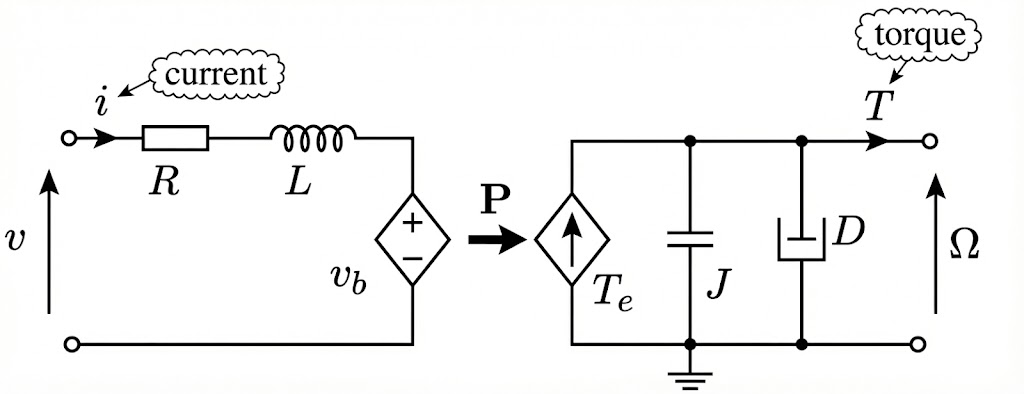
例子：DC Motor